Backpacking through Europe

This article is a part of a series intended to show users how to use Memgraph on real-world data and, by doing so, retrieve some interesting and useful information.

We highly recommend checking out the other articles from this series which are listed in our tutorial overview section.

Introduction

Backpacking is a form of low-cost independent travel. It includes the use of public transportation, inexpensive hostels and is often longer in duration than conventional vacations. This article explores the European Backpackers Index from 2018. The dataset contains tourist prices and other data for 56 of the most popular European cities. Here we showcase how Memgraph's graph traversal algorithms can be used to make a real-time travelling recommendation system.

Data model

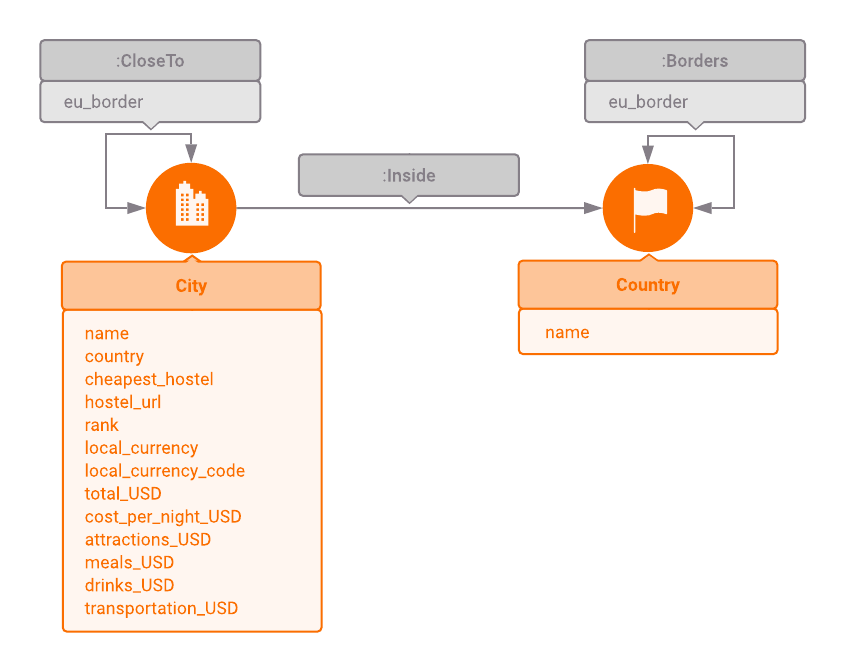
The European Backpacker Index (2018) contains information for 56 cities from 36 European countries. Two cities are connected via the :CloseTo edge if they are from the same or from the neighboring countries. Every edge has an eu_border property to indicate whether the EU border needs to be crossed to reach the other city. The index lists the cheapest and most attractive hostel from each city. The hostel name can be accessed via the cheapest_hostel parameter, and its website is stored in hostel_url. The city nodes also contain parameters for tourist information such as local_currency, local_currency_code, and total_USD. total_USD is the sum of the most common tourist expenses, such as cost_per_night_USD, attractions_USD, drinks_USD, meals_USD, and transportation_USD. The country nodes are connected with the :Borders edge if they are neighboring countries. This edge also has the eu_border property. Every city node is connected to its parent country node via the :Inside edge.

Exploring the dataset

You have two options for exploring this dataset. If you just want to take a look at the dataset and try out a few queries, open Memgraph Playground and continue with the tutorial there. Note that you will not be able to execute write operations.

On the other hand, if you would like to add changes to the dataset, download the Memgraph Lab desktop application and navigate to the Datasets tab in the sidebar. From there, choose the dataset Backpacking through Europe and continue with the tutorial.

Example queries

1) Let's list the top 10 cities with the cheapest hostels by cost per night from the European Backpacker Index.

MATCH (n:City)
RETURN n.name, n.cheapest_hostel, n.cost_per_night_USD, n.hostel_url
ORDER BY n.cost_per_night_USD LIMIT 10;

2) Say we want to visit Croatia. Which cities does Backpackers Index recommend? Let's sort them by total costs.

MATCH (c:City)-[:Inside]->(:Country {name: "Croatia"})
RETURN c.name, c.cheapest_hostel, c.total_USD
ORDER BY c.total_USD;

3) What if we want to visit multiple cities in a single country and want to know which country has the most cities in the index?

MATCH (n:Country)<-[:Inside]-(m:City)
RETURN n.name AS CountryName, COUNT(m) AS HostelCount
ORDER BY HostelCount DESC, CountryName LIMIT 10;

Now, let's start backpacking. This is where Memgraph's graph traversal capabilities come into play.

4) We're on a trip from Spain to Russia and want to cross the least amount of borders. This is a great job for the breadth-first search (BFS) algorithm.

MATCH p = (n:Country {name: "Spain"})
          -[r:Borders * bfs]-
          (m:Country {name: "Russia"})
UNWIND (nodes(p)) AS rows
RETURN rows.name;

5) What if we're interested in going from Bratislava to Madrid with the least amount of stops? Also, we can't be bothered to switch currencies and want to pay with Euro everywhere along the trip.

MATCH p = (:City {name: "Bratislava"})
          -[:CloseTo * bfs (e, v | v.local_currency = "Euro")]-
          (:City {name: "Madrid"})
UNWIND (nodes(p)) AS rows
RETURN rows.name;

Here we can see how to use the filter lambda to filter paths where the local currency in the city vertex v is the Euro. nodes(p) returns the path as a list, and UNWIND unpacks the list into individual rows.

6) This time we're going from Brussels to Athens on a budget. We're interested in the route with the cheapest stays. But there's a problem, we've lost our passport! Luckily, we're a European Union citizen and can travel freely within the EU. Let's find the cheapest route from Brussels to Athens with no EU border crossings. This is a good use case for the Dijkstra's shortest path algorithm.

MATCH p = (:City {name: "Brussels"})
          -[:CloseTo * wShortest(e, v | v.cost_per_night_USD) total_cost (e, v | e.eu_border=FALSE)]-
          (:City {name: "Athens"})
WITH extract(city in nodes(p) | city.name) AS trip, total_cost
RETURN trip, total_cost;

Here we used the weight lambda to specify the cost of expanding to the specified vertex using the given edge (v.cost_per_night_USD), and the total cost symbol to calculate the cost of the trip. This can be done using an edge property like in the Exploring the European Road Network tutorial. Here we use cost_per_night property of the city vertex v as our weight. Finally, we use the filter lambda to only consider paths with no EU border crossings. The extract function is used to only show the city names. To get the full city information, we would simply return nodes(p).

7) We're on a trip with our friends from Madrid to Belgrade, but want to visit Vienna along the way. We want to party it up on the first part of our trip and are only interested in the cost of staying and drinks. After that, we plan on sightseeing and are interested in the cost of attractions from Vienna to Belgrade. What is our cheapest option?

MATCH p = (:City {name: "Madrid"})
          -[:CloseTo * wShortest(e, v | v.cost_per_night_USD + v.drinks_USD) cost1]-
          (:City {name: "Vienna"})
          -[:CloseTo * wShortest(e, v | v.cost_per_night_USD + v.attractions_USD) cost2]-
          (:City {name: "Belgrade"})
WITH extract(city in nodes(p) | city.name) AS trip, cost1, cost2
RETURN trip, cost1 + cost2 AS total_cost;

8) We're on a trip from Paris to Zagreb and want to visit at least 3 cities, but no more than 5 (excluding the starting location — Paris). Let's list our top 10 options sorted by the total trip cost and number of cities in the path.

MATCH path = (n:City {name: "Paris"})-[:CloseTo *3..5]-(m:City {name: "Zagreb"})
WITH nodes(path) AS trip
WITH extract(city in trip | [city, trip]) AS lst
UNWIND lst AS rows
WITH rows[0] AS city, extract(city in rows[1] | city.name) AS trip
RETURN trip,
       toInteger(sum(city.total_USD)) AS trip_cost_USD,
       count(trip) AS city_count
ORDER BY trip_cost_USD, city_count DESC LIMIT 10;

Here we can see the usage of the variable length paths. By using the * (asterisk) symbol, we can traverse from one node to another by following any number of connections. We then use the extract function to get a list of (city, trip) tuples. The city is used to calculate the total cost of the trip using the sum function. Finally, we sort our results by price first, and then by city count.

To learn more about these algorithms, we suggest you check out their Wikipedia pages:

• Breadth-first search
• Dijkstra's algorithm