Graph algorithms

Introduction

A graph is a mathematical structure used to describe a set of objects in which certain pairs of objects are "related" in some sense. Generally, we consider those objects as abstractions named nodes (also called vertices) and the relations between them as an abstractions named relationships (also called edges).

It turns out that a lot of real-world problems can be successfully modeled using graphs. Some natural examples would contain railway networks between cities, computer networks, piping systems and Memgraph itself.

This article outlines some of the most important graph algorithms that are internally used by Memgraph you could significantly benefit from. Please keep in mind that this article does not contain an in-depth analysis of algorithms and their implementation details since those are well documented in the appropriate literature and, in our opinion, go well out of scope of user documentation. What this article does contain is the relevant information for using Memgraph effectively and efficiently.

This article outlines:

• Breadth-first search (BFS)
• Weighted shortest path (WSP)

Memgraph has a lot more graph algorithms to offer besides these two and they are all a part of MAGE.

Breadth-first search

Breadth-first search is a way of traversing a graph data structure. The traversal starts from a single node (usually referred to as source node) and, during the traversal, breadth is prioritized over depth, hence the name of the algorithm. More precisely, when we visit some node, we can safely assume that we have already visited all nodes that are fewer relationships away from a source node. An interesting side-effect of traversing a graph in BFS order is the fact that, when we visit a particular node, we can easily find a path from the source node to the newly visited node with the least number of relationships. Since in this context we disregard the relationship weights, we can say that BFS is a solution to an unweighted shortest path problem.

The algorithm itself proceeds as follows:

• Keep around a set of nodes that are equidistant from the source node. Initially, this set contains only the source node.
• Expand to all not yet visited nodes that are a single relationship away from that set. Note that the set of those nodes is also equidistant from the source node.
• Replace the set with a set of nodes obtained in the previous step.
• Terminate the algorithm when the set is empty.

The order of visited nodes is nicely visualized in the following animation from Wikipedia. Note that each row contains nodes that are equidistant from the source and thus represents one of the sets mentioned above.

The standard BFS implementation skews from the above description by relying on a FIFO (first in, first out) queue data structure. Nevertheless, the functionality is equivalent and its runtime is bounded by O(|V| + |E|) where V denotes the set of nodes and E denotes the set of relationships. Therefore, it provides a more efficient way of finding unweighted shortest paths than running Dijkstra's algorithm on a graph with relationship weights equal to 1.

Here is an example of finding the shortest path between nodes:

MATCH (a {id: 723})-[edge_list:Type *bfs..10]-(b {id: 882}) RETURN *;

The above query will find all paths of length up to 10 between nodes a and b. The edge type and maximum path length are used in the same way as in variable length expansion.

To find only the shortest path, simply append LIMIT 1 to the RETURN clause.

MATCH (a {id: 723})-[edge_list:Type *bfs..10]-(b {id: 882}) RETURN * LIMIT 1;

Breadth-first expansion allows an arbitrary expression filter that determines if an expansion is allowed. Following is an example in which expansion is allowed only over edges whose x property is greater than 12 and nodes y whose property is less than 3:

MATCH (a {id: 723})-[*bfs..10 (e, n | e.x > 12 AND n.y < 3)]-() RETURN *;

The filter is defined as a lambda function over e and n, which denote the edge and node being expanded over in the breadth first search. If you omit the edge list symbol (edge_list in previous examples) it will not be included in the result.

Weighted Shortest Path

In graph theory, weighted shortest path problem is the problem of finding a path between two nodes in a graph such that the sum of the weights of relationships connecting nodes on the path is minimized.

Dijkstra's algorithm

One of the most important algorithms for finding weighted shortest paths is Dijkstra's algorithm. Our implementation uses a modified version of this algorithm that can handle length restriction. The length restriction parameter is optional and when it's not set it could increase the complexity of the algorithm. It is important to note that the term "length" in this context denotes the number of traversed relationships and not the sum of their weights.

The algorithm itself is based on a couple of greedy observations and could be expressed in natural language as follows:

• Keep around a set of already visited nodes along with their corresponding shortest paths from source node. Initially, this set contains only the source node with the shortest distance of 0.
• Find an relationship that goes from a visited node to an unvisited one such that the shortest path from source to the visited node increased by the weight of that relationship is minimized. Traverse that relationship and add a newly visited node with appropriate distance to the set of already visited nodes.
• Repeat the process until the destination node is visited.

The described algorithm is nicely visualized in the following animation from Wikipedia. Note that relationship weights correspond to the Euclidean distance between nodes which represent points on a plane.

Using appropriate data structures the worst-case performance of our implementation can be expressed as O(|E| + |V|log|V|) where E denotes the set of relationships and V denotes the set of nodes.

A sample query that finds a shortest path between two nodes looks as follows:

MATCH (a {id: 723})-[edge_list *wShortest 10 (e, n | e.weight) total_weight]-(b {id: 882}) RETURN *;

This query has an upper bound length restriction set to 10. This means that no path that traverses more than 10 relationships will be considered as a valid result.

Upper Bound Implications

Since the upper bound parameter is optional, we can have different results based on this parameter.

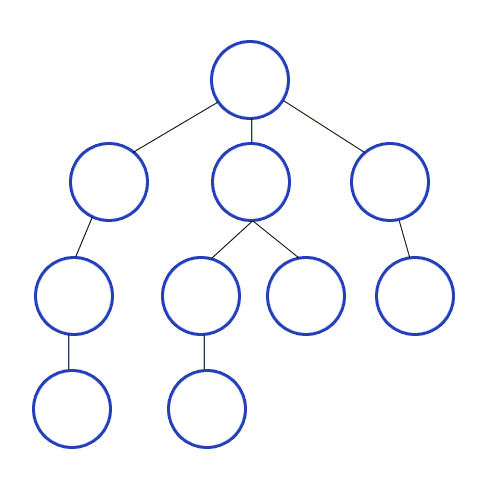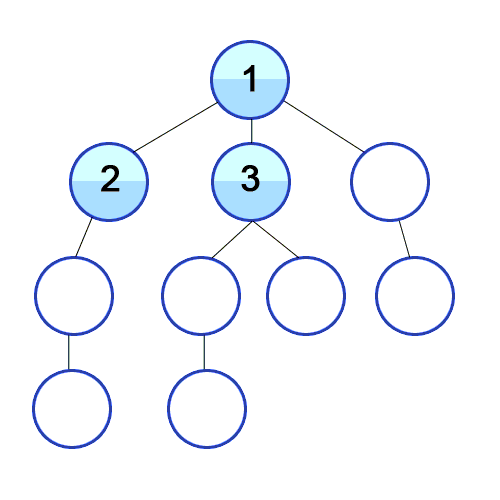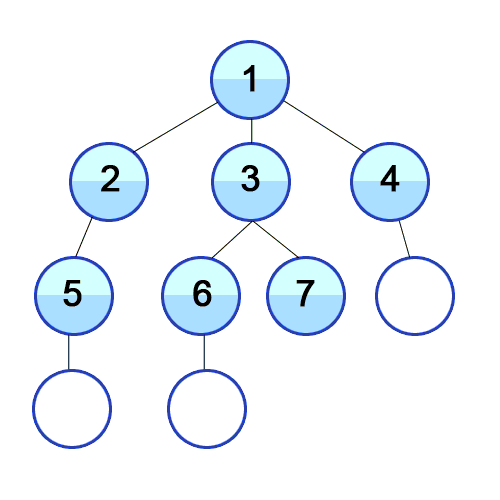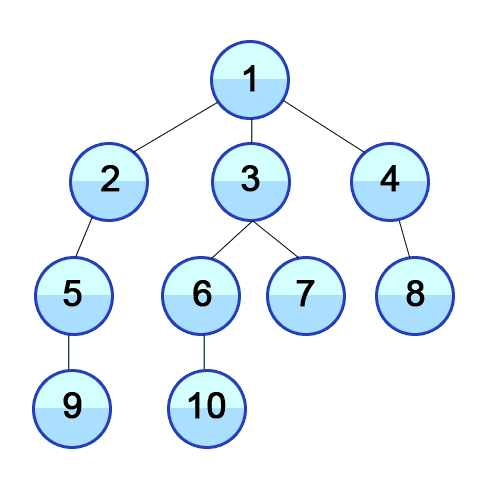
Consider the following graph and sample queries.

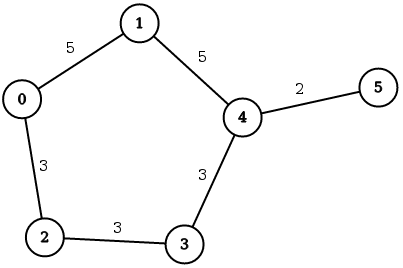
MATCH (a {id: 0})-[edge_list *wShortest 3 (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *;

MATCH (a {id: 0})-[edge_list *wShortest   (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *;

The first query will try to find the weighted shortest path between nodes 0 and 5 with the restriction on the path length set to 3, and the second query will try to find the weighted shortest path with no restriction on the path length.

The expected result for the first query is 0 -> 1 -> 4 -> 5 with the total cost of 12, while the expected result for the second query is 0 -> 2 -> 3 -> 4 -> 5 with the total cost of 11. Obviously, the second query can find the true shortest path because it has no restrictions on the length.

To handle cases when the length restriction is set, weighted shortest path algorithm uses both node and distance as the state. This causes the search space to increase by the factor of the given upper bound. On the other hand, not setting the upper bound parameter, the search space might contain the whole graph.

Because of this, one should always try to narrow down the upper bound limit to be as precise as possible in order to have a more performant query.

Where to next?

For some real-world application of WSP we encourage you to visit our article Exploring the European road network which was specially crafted to showcase our graph algorithms.