Storage memory usage
Estimating Memgraph's storage memory usage is not entirely straightforward because it depends on a lot of variables, but it is possible to do so quite accurately. Below is an example that will try to show the basic reasoning.
If you want to estimate the storage memory usage, use the following formula:
Let's test this formula on the Marvel Comic Universe Social Network dataset, which is also available as a dataset inside Memgraph Lab and contains 21,723 vertices and 682,943 edges.
According to the formula, storage memory usage should be:
Now, let's run an empty Memgraph instance on a x86 Ubuntu. It consumes ~75MB
of RAM due to baseline runtime overhead. Once the dataset is loaded, RAM usage
rises up to ~260MB. Memory usage primarily consists of storage and query
execution memory usage. After executing FREE MEMORY query to force the cleanup
of query execution, the RAM usage drops to ~200MB. If the baseline runtime
overhead of 75MB is subtracted from the total memory usage of the dataset,
which is 200MB, and storage memory usage comes up to ~125MB, which shows
that the formula is correct.
The calculation in detail
Let's dive deeper into the memory usage values. Because Memgraph works on the x86 architecture, calculations are based on the x86 Linux memory usage.
Each Vertex and Edge object has a pointer to a Delta object. The
Delta object stores all changes on a certain Vertex or Edge and that's
why Vertex and Edge memory usage will be increased by the memory of
the Delta objects they are pointing to. If there are few updates, there are
also few Delta objects because the latest data is stored in the object.
But, if the database has a lot of concurrent operations, many Delta objects
will be created. Of course, the Delta objects will be kept in memory as long as
needed, and a bit more, because of the internal GC inefficiencies.
Delta memory layout
Each Delta object has a least 104B.
Vertex memory layout
Each Vertex object has at least 112B + 104B for the Delta object, in
total, a minimum of 216B.
Edge memory layout
Each Edge object has at least 40B + 104B for the Delta object, in
total, a minimum of 144B.
SkipList memory layout
Each object (Vertex, Edge) is placed inside a data structure
called a SkipList. The SkipList has an additional overhead in terms of
SkipListNode structure and next_pointers. Each SkipListNode has an
additional 8B element overhead and another 8B for each of the next_pointers.
It is impossible to know the exact number of next_pointers upfront, and consequently the total size, but it's never more than double the number of objects because the number of pointers is generated by binomial distribution (take a look at the source code for details).
Index memory layout
Each LabelIndex::Entry object has exactly 16B.
Depending on the actual value stored, each LabelPropertyIndex::Entry has at least 72B.
Objects of both types are placed into the SkipList.
Each index object in total
SkipListNode<LabelIndex::Entry>object has 24B.SkipListNode<LabelPropertyIndex::Entry>has at least 80B.- Each
SkipListNodehas an additional 16B because of the next_pointers.
Properties
All properties use 1B for metadata - type, size of property ID and the size
of payload in the case of NULL and BOOLEAN values, or size of payload size
indicator for other types (how big is the stored value, for example, integers
can be 1B, 2B 4B or 8b depending on their value).
Then they take up another byte for storing property ID, which means each
property takes up at least 2B. After those 2B, some properties (for example,
STRING values) store addition metadata. And lastly, all properties store the
value. So the layout of each property is:
| Value type | Size | Note |
|---|---|---|
NULL | 1B + 1B | The value is written in the first byte of the basic metadata. |
BOOL | 1B + 1B | The value is written in the first byte of the basic metadata. |
INT | 1B + 1B + 1B, 2B, 4B or 8B | Basic metadata, property ID and the value depending on the size of the integer. |
DOUBLE | 1B + 1B + 8B | Basic metadata, property ID and the value |
STRING | 1B + 1B + 1B + min 1B | Basic metadata, property ID, additional metadata and lastly the value depending on the size of the string, where 1 ASCII character in the string takes up 1B. |
LIST | 1B + 1B + 1B + min 1B | Basic metadata, property ID, additional metadata and the total size depends on the number and size of the values in the list. |
MAP | 1B + 1B + 1B + min 1B | Basic metadata, property ID, additional metadata and the total size depends on the number and size of the values in the map. |
TEMPORAL_DATA | 1B + 1B + 1B + min 1B + min 1B | Basic metadata, property ID, additional metadata, seconds, microseconds. Value od the seconds and microseconds is at least 1B, but probably 4B in most cases due to the large values they store. |
Marvel dataset use case
The Marvel dataset consists of Hero, Comic and ComicSeries labels, which
are indexed. There are also three label-property indices - on the name
property of Hero and Comic vertices, and on the title property of
ComicSeries vertices. The ComicSeries vertices also have the publishYear
property.
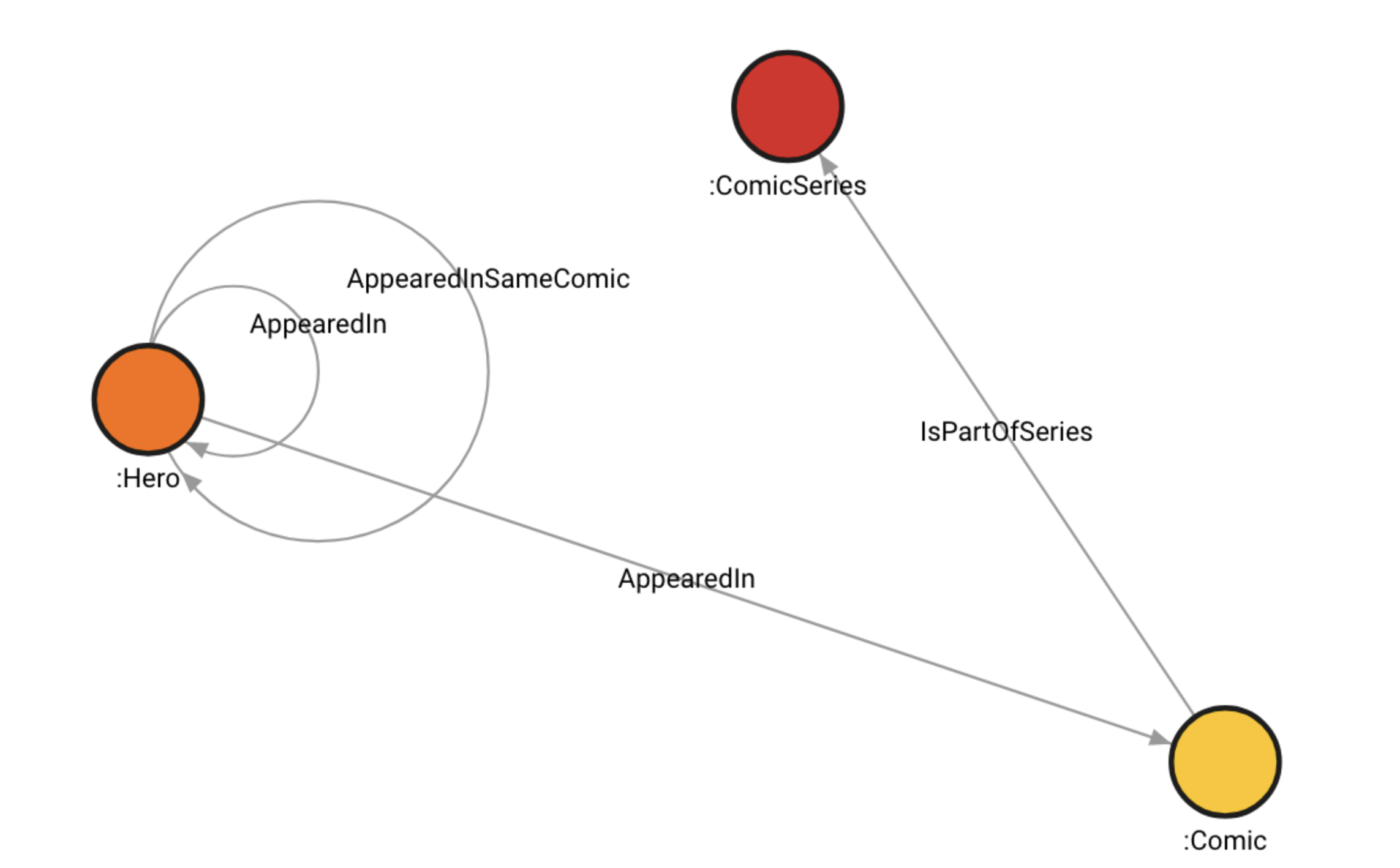
There are 6487 Hero and 12,661 Comic vertices with the property name.
That's 19,148 vertices in total. To calculate how much storage those vertices
and properties occupy, we are going to use the following formula:
Let's assume the name on average has (each name is on average 10 characters long). One the average values are included, the calculation is:
The remaining 2,584 vertices are the ComicSeries vertices with the title and
publishYear properties. Let's assume that the title property is
approximately the same length as the name property. The publishYear property
is a list of integers. The average length of the publishYear list is 2.17,
let's round it up to 3 elements. Since the year is an integer, 2B for each
integer will be more than enough, plus the 2B for the metadata. Therefore, each
list occupies . Using the same
formula as above, but being careful to include both title and publishYear
properties, the calculation is:
In total, to store vertices.
The edges don't have any properties on them, so the formula is as follows:
There are 682,943 edges in the Marvel dataset. Hence, we have:
Next, Hero, Comic and ComicSeries labels have label indices. To calculate
how much space they take up, use the following formula:
Since there are three label indices, we have the following calculation:
For label-property index, labeled property needs to be taken into account.
Property name is indexed on Hero and Comic vertices, while property
title is indexed on ComicSeries vertices. We already assumed that the
title property is approximately the same length as the name property.
Here is the formula:
When the appropriate values are included, the calculation is:
Now let's sum up everything we calculated:
Bear in mind the number can vary because objects can have higher overhead due to the additional data.
Query Execution memory Usage
Query execution also uses up RAM. In some cases, intermediate results are aggregated to return valid query results and the query execution memory can end up using a large amount of RAM. Keep in mind that query execution memory monotonically grows in size during the execution, and it's freed once the query execution is done.
Configuration options to reduce memory usage
Here are several tips how you can reduce memory usage and increase scalability:
- Consider removing label index by executing
DROP INDEX ON :Label; - Consider removing label-property index by executing
DROP INDEX ON :Label(property); - If you don't have properties on relationships, disable them in the
configuration file by setting the
-storage-properties-on-edgesflag tofalse. This can significantly reduce memory usage because effectivelyEdgeobjects will not be created, and all information will be inlined underVertexobjects. You can disable properties on relationships with a non-empty database, if the relationships are without properties. If you need help with adapting the configuration to your needs, check out the the how-to guide on changing configuration settings.
You can also check our reference guide for information about controlling memory usage, and you inspect and profile your queries to devise a plan for their optimization.